Monty Hall Simulation

I recently watched a video explaining the Monty Hall problem, and thought it would be fun to write a small Python program that proves that the less-than-obvious approach of switching your chosen door leads to higher probability of success.

First, we’ll need to bring in the necessary libraries:

from random import randint
import matplotlib.pyplot as plt

Next, we’ll define the number of games we’re going to play. Because this is a statistical simulation, we’re interested in the overall trends that arise after a large number of observations:

# we'll start with 50 so that our
# visualizations are easier to read,
# and maybe increase it later 
N_ROUNDS = 50

We’ll also need some variables to keep track of the games results. Remember, we’re evaluating the difference between the following approaches:

1. STAY with the first door we chose
2. SWITCH to the unopened door

stay_wins = 0
switch_wins = 0
stay_record = []
switch_record = []

Time to play the game! Let’s set up the for loop that will simulate playing one game after another:

for _n in range(N_ROUNDS):

At the beginning of each game, one of the doors are randomly selected to hide the “prize”, and we (the contestant) are also going to randomly select a door:

    prize = randint(1, 3)
    choice = randint(1, 3)

Now for the madness. Monty is going to open a door that ISN’T the door we chose, OR the door that is hiding the prize. We’ll do this with a list comprehension:

    # NOTE the [0] at the end. list comprehensions
    # return a list, but we just want the single element
    open_door = [x for x in [1,2,3] if x not in (prize, choice)][0]

Next, we need to identify the “alternate door” that we have the opportunity to switch to. This alt_door will be the door that ISN’T the one we originally chose OR the newly opened door:

    alt_door = [x for x in [1,2,3] if x not in (choice, open_door)][0]

Now for the easy part! We will evaluate the result of the two strategies. If the door we first chose is the same door that is hiding the prize, the STAY strategy was successful. If the alternate door happens to be the prize door, then the SWITCH door was correct:

    if choice == prize:
        stay_wins += 1
    stay_record.append(stay_wins)

    if alt_door == prize:
        switch_wins += 1
    switch_record.append(switch_wins)

That’s it! We can exit the loop and do some final calculations:

stay_pct = round(stay_wins / N_ROUNDS, 2)
switch_pct = round(switch_wins / N_ROUNDS, 2)

And for the final step, we can plot the two approaches and see how they compare over time:

plt.scatter(range(N_ROUNDS), stay_record, c='red', label=f'STAY')
plt.scatter(range(N_ROUNDS), switch_record, c='blue', label='SWITCH')
plt.xlabel('number of games')
plt.ylabel('number of wins')
plt.title(f'STAY: {stay_pct}%; SWITCH: {switch_pct}%')
plt.legend()
plt.show()

Your plot should look something like this:

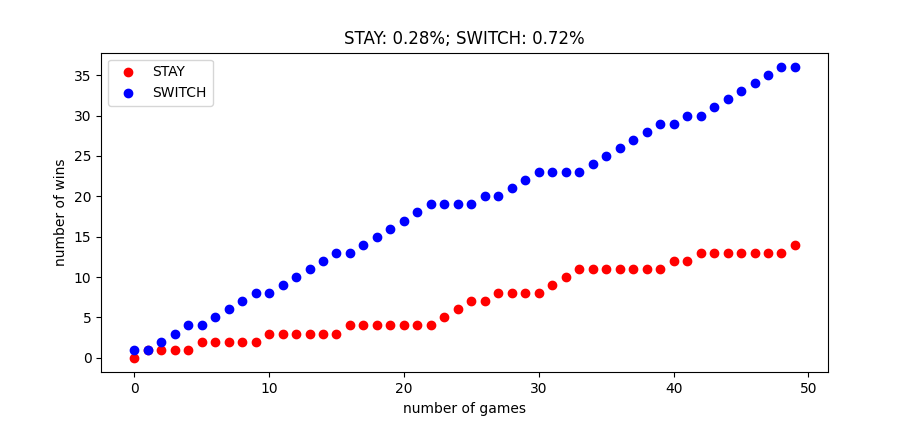
The exact results will vary, but you should notice that the SWITCH strategy is about twice as more successful than the STAY strategy. As we increase N_ROUNDS, the STAY and SWITCH success rates will approach 0.33 and 0.67 respectively, which is the theoretical probability estimated from the video.

Full Script

from random import randint
import matplotlib.pyplot as plt

N_ROUNDS = 50

stay_wins = 0
switch_wins = 0
stay_record = []
switch_record = []

for _n in range(N_ROUNDS):
    prize = randint(1, 3)
    choice = randint(1, 3)

    # simulate Monty opening the door by selecting the door that 
    # is not the prize, and not the one selected by the player
    open_door = [x for x in [1,2,3] if x not in (prize, choice)][0]

    # which means, the alternate door (the door the player can switch
    # too) is the door that is not their own, and not the one that has been opened
    alt_door = [x for x in [1,2,3] if x not in (choice, open_door)][0]

    # evaluate success using the "stay strategy"
    if choice == prize:
        stay_wins += 1
    stay_record.append(stay_wins)

    # evaluate success using the "switch strategy"
    if alt_door == prize:
        switch_wins += 1
    switch_record.append(switch_wins)


stay_pct = round(stay_wins / N_ROUNDS, 2)
switch_pct = round(switch_wins / N_ROUNDS, 2)

plt.scatter(range(N_ROUNDS), stay_record, c='red', label=f'STAY')
plt.scatter(range(N_ROUNDS), switch_record, c='blue', label='SWITCH')
plt.xlabel('number of games')
plt.ylabel('number of wins')
plt.title(f'STAY: {stay_pct}%; SWITCH: {switch_pct}%')
plt.legend()
plt.show()